Nesse artigo será abordado a teoria completa de Progressão Geométrica com exemplos para um melhor aprendizado da teoria.
Progressão Geométrica
Chamamos Progressão Geométrica (P.G.) a uma seqüência de números reais, formada por termos, que a partir do 2º, é igual ao produto do anterior por uma constante q dada, chamada de razão da P.G.
Dada uma seqüência (a1, a2, a3, a4, ..., an,...), então se ela for uma P.G.  an = an-1 . q , com n
an = an-1 . q , com n 2 e n
2 e n IN, onde:
IN, onde:
a1 – 1º termo
a2 = a1. q 

a3 = a2. q² 

a4 = a3. q³ 
 .
.
an = an-1. q 

CLASSIFICAÇÃO DAS PROGRESSÕES GEOMÉTRICAS P.G.s
1. Crescente:

2. Decrescente:

3. Alternante ou Oscilante: quando q < 0.
4. Constante: quando q = 1
5. Estacionária ou Singular: quando q = 0
FÓRMULA DO TERMO GERAL DE UMA PROGRESSÃO GEOMÉTRICA
Vamos considerar uma P.G. (a1, a2, a3, a4,..., an,...). Pela definição temos:
a1 = a1
a2 = a1. q 

a3 = a2. q² 

a4 = a3. q³ 
 .
.
an = an-1. q 

Depois de multiplicarmos os dois membros das igualdades e simplificarmos, vem:
an = a1.q.q.q....q.q
(n-1 fatores)
Exemplo 1:
Dada a PG (2,4,8,... ), pede-se calcular o décimo termo.
Temos: a1 = 2, q = 4/2 = 8/4 = ... = 2. Para calcular o décimo termo ou seja a10, vem pela fórmula:
a10 = a1 . q9 = 2 . 29 = 2. 512 = 1024
Exemplo 2:
Sabe-se que o quarto termo de uma PG crescente é igual a 20 e o oitavo termo é igual a 320. Qual a razão desta PG?
Solução:Temos a4 = 20 e a8 = 320. Logo, podemos escrever: a8 = a4 . q8-4 . Daí, vem: 320 = 20.q4
Então q4 =16 e portanto q = 2.
Então q4 =16 e portanto q = 2.
Nota: Uma PG genérica de 3 termos, pode ser expressa como:
(x/q, x, xq), onde q é a razão da PG.
(x/q, x, xq), onde q é a razão da PG.
INTERPOLAÇÃO GEOMÉTRICA
Interpolar, Inserir ou Intercalar m meios geométricos entre dois números reais a e b significa obter uma P.G. de extremos a e b, com m+2 elementos. Podemos resumir que problemas envolvendo interpolação se reduzem em calcularmos a razão da P.G.
Exemplo 1:


Exemplo 1:
Uma PG é formada por 6 termos, onde a1 = 4 e a6 = 972. Determine os meios geométricos existentes entre a1 e a6.
Solução:
Para interpolar os meios geométricos entre 4 e 972 precisamos determinar o valor da razão da PG. Para isso, vamos utilizar a fórmula do termo geral.

Sabemos que a razão da PG é 3 e que cada termo, a partir do segundo, é obtido fazendo o produto entre o termo anterior e a razão. Assim, teremos:

Sabemos que a razão da PG é 3 e que cada termo, a partir do segundo, é obtido fazendo o produto entre o termo anterior e a razão. Assim, teremos:

Exemplo 2:
Uma indústria produziu 100 unidades de um produto no mês de janeiro. Em julho do mesmo ano, ela produziu 6400 unidades desse produto. Determine quantas unidades foram produzidas nos meses de fevereiro a junho, sabendo que as quantidades produzidas de janeiro a julho determinam uma PG.
Solução:
Solução:
De acordo com o enunciado do problema, a sequência (100, _, _, _, _, _, 6400) é uma P.G. Para resolver o problema precisamos determinar os termos que faltam nessa P.G ou interpolar meios geométricos entre 100 e 6400. Assim, precisamos determinar a razão dessa P.G, onde a1 = 100 e a7 = 6400.

Conhecido o valor da razão, temos que:

Conhecido o valor da razão, temos que:

Portanto, a produção no mês de fevereiro foi de 200 unidades; março foi de 400 unidades; abril foi de 800 unidades; maio foi de 1600 unidades; e junho foi de 3200 unidades.
SOMA DOS TERMOS DE UMA P.G. FINITA
Dada a P.G. (a1, a2, a3, a4, ..., an-1, an...), de razão  e a soma Sn de seus n termos pode ser expressa por:
e a soma Sn de seus n termos pode ser expressa por:
Sn = a1+a2+a3+a4... +an(Eq.1) Multiplicando ambos os membros por q, vem:
q.Sn = (a1+a2+a3+a4... +an).q
q.Sn = a1.q+a2.q+a3 +.. +an.q (Eq.2) . Encontrando a diferença entre a (Eq.2) e a (Eq.1),
temos:

q.Sn - Sn = an . q - a1
Obs.: Se a P.G. for constante, isto é, q = 1 a soma Sn será:
Exemplo:
Dê a soma dos termos da seguinte PG (7,14,28, ... , 3584).
Para utilizarmos a fórmula da soma é preciso saber quem é o 1º termo, a razão e a quantidade de elementos que essa PG possui.
a1 = 7
q = 2
n = ?
Sn = ?
Portanto, é preciso que encontremos a quantidade de elementos que possui essa PG, utilizando a fórmula do termo geral.
an = a1 . qn – 1
3584 = 7 . 2n – 1
3584 : 7 = 2n – 1
512 = 2n – 1
29 = 2n – 1
n – 1 = 9
n = 10
Sn = a1 (qn – 1)
q - 1
S10 = 7 (210 – 1)
2 – 1
S10 = 7 (1024 – 1)
2 – 1
S10 = 7 . 1023
S10 = 7161
SOMA DOS TERMOS DE UMA P.G. INFINITA
Dada a P.G. infinita: (a1, a2, a3, a4, ...), de razão q e S sua soma, devemos analisar 3 casos para calcularmos a soma S.
an = a1.
1. Se a1= 0  S = 0, pois
S = 0, pois
2. Se q <–1 ou q > 1, isto é  e a1
e a1 0, S tende a
0, S tende a  ou
ou  . Neste caso é impossível calcular a soma S dos termos da P.G.
. Neste caso é impossível calcular a soma S dos termos da P.G.
3. Se –1< q < 1, isto é,  e a1
e a1 0, S converge para um valor finito. Assim a partir da Fórmula da soma dos n termos de uma P.G. , vem:
0, S converge para um valor finito. Assim a partir da Fórmula da soma dos n termos de uma P.G. , vem:
Quando n tende a  , qn tende a zero, logo:
, qn tende a zero, logo:
Obs.: S nada mais é do que o limite da Soma dos termos da P.G., quando n tende para  É representada desta forma:
É representada desta forma:
Exemplo:
Determine a soma dos elementos da progressão geométrica dada por (0,3; 0,03; 0,003; 0,0003; ...).
.jpg)
.jpg)
PRODUTO DOS TERMOS DE UMA P.G. FINITA
.jpg)
.jpg)
Dada a P.G. finita: (a1, a2, a3, ...an-1, an), de razão q e P seu produto, que é dado por:
Multiplicando membro a membro, vem:

Podemos também escrever esta fórmula de outra forma, pois:

Logo:

Exemplo:
Obtenha o produto dos seis primeiros termos da PG (4,8,16,......)
a6= a1.q5 => a6 = 4.25 => a6 = 128
P6 =(a1.a6)6/2 P6 =(4.128)3 => P6 = 5123
Fontes: http://www.algosobre.com.br
Questões resolvidas e propostas
1) (FUVEST/01) Uma progressão aritmética e uma progressão geométrica têm, ambas, o primeiro termo igual a 4, sendo que os seus terceiros termos são estritamente positivos e coincidem. Sabe-se ainda que o segundo termo da progressão aritmética excede o segundo termo da progressão geométrica em 2. Então, o terceiro termo das progressões é:
a) 10
b) 12
c) 14
d) 16
e) 18
Solução:
Sejam (a1, a2, a3, …) a PA de razão r e (g1, g2, g3, …) a PG de razão q. Temos como condições iniciais:
(1) a1 = g1 = 4
(2) a3 > 0, g3 > 0 e a3 = g3
(3) a2 = g2 + 2
Reescrevendo (2) e (3) utilizando as fórmulas gerais dos termos de uma PA e de uma PG e (1) obtemos o seguinte sistema de equações:
4) a3 = a1 + 2r e g3 = g1.q2 => 4 + 2r = 4q2
(5) a2 = a1 + r e g2 = g1.q => 4 + r = 4q + 2
Expressando, a partir da equação (5), o valor de r em função de q e substituindo r em (4) vem:
(5) => r = 4q + 2 - 4 => r = 4q - 2
(4) => 4 + 2(4q - 2) = 4q2 => 4 + 8q - 4 = 4q2 => 4q2 - 8q = 0
=> q(4q - 8) = 0 => q = 0 ou 4q - 8 = 0 => q = 2
Como g3 > 0, q não pode ser zero e então q = 2. Para obter r basta substituir q na equação (5):
r= 4q - 2 => r = 8 - 2 = 6
Para concluir calculamos a3 e g3:
a3 = a1 + 2r => a3 = 4 + 12 = 16
g3 = g1.q2 => g3 = 4.4 = 16
2) (MACK) O sexto termo de uma PG, na qual dois meios geométricos estão inseridos entre 3 e -24, tomados nessa ordem, é:
a) -48
b) -96
c) 48
d) 96
e) 192
Solução:
Para determinar os dois meios geométricos da PG cujos extremos são 3 e -24 precisamos calcular, primeiro, sua razão q, com n = 4. Pela fórmula do termo geral temos que:
a4 = a1.q4-1 => -24 = 3q3 => q3 = -24/3 = -8 => q = -2
Logo a PG é (3; -6; 12; -24; …) e seu sexto termo é obtido, também, através da fórmula do termo geral:
a6 = a1q6-1 => a6 = 3(-2)5 = -3.32 = -96
3) (UE – PA) Um carro, cujo preço à vista é R$ 24 000,00, pode ser adquirido dando-se uma entrada e o restante em 5 parcelas que se encontram em progressão geométrica. Um cliente que optou por esse plano, ao pagar a entrada, foi informado que a segunda parcela seria de R$ 4 000,00 e a quarta parcela de R$ 1 000,00. Quanto esse cliente pagou de entrada na aquisição desse carro?
Solução:
an = a1 * q n–1
a2 = 4000
a4 = 1000
a4 = 1000
a2 = a1 * q
4000 = a1 * q
a1 = 4000 / q
4000 = a1 * q
a1 = 4000 / q
a4 = a1 * q3
1000 = 4000 / q * q3
1000 / 4000 = q3 / q
1 / 4 = q2
√1/4 = √q2
q = 1/2
1000 = 4000 / q * q3
1000 / 4000 = q3 / q
1 / 4 = q2
√1/4 = √q2
q = 1/2
a1 = 4000 / 1/2
a1 = 4000 * 2
a1 = 8000
a1 = 4000 * 2
a1 = 8000
1ª prestação: R$ 8 000,00
2ª prestação: R$ 4 000,00
3ª prestação: R$ 2 000,00
4ª prestação: R$ 1 000,00
5ª prestação: R$ 500,00
2ª prestação: R$ 4 000,00
3ª prestação: R$ 2 000,00
4ª prestação: R$ 1 000,00
5ª prestação: R$ 500,00
Soma total das prestações: R$ 15 500,00
Entrada (valor do carro menos o total das prestações)
R$ 24 000,00 – R$ 15 500,00 = R$ 8 500,00
O valor da entrada foi de R$ 8 500,00
4) O limite da expressão  onde x é positivo, quando o número de radicais aumenta indefinidamente
onde x é positivo, quando o número de radicais aumenta indefinidamente
é igual a:
A)1/x
*B) x
C) 2x
D) n.x
E) 1978x
*B) x
C) 2x
D) n.x
E) 1978x
Solução:
Observe que a expressão dada pode ser escrita como:
x1/2. x1/4 . x1/8 . x1/16 . ... = x1/2 + 1 / 4 + 1/8 + 1/16 + ...
Observe que a expressão dada pode ser escrita como:
x1/2. x1/4 . x1/8 . x1/16 . ... = x1/2 + 1 / 4 + 1/8 + 1/16 + ...
O expoente é a soma dos termos de uma PG infinita de primeiro termo a1 = 1 /2 e
razão q = 1 /2. Logo, a soma valerá: S = a1 / (1 – q) = (1 /2) / 1 – (1 /2) = 1
Então, x1/2 + 1 / 4 + 1/8 + 1/16 + ... = x1 = x
razão q = 1 /2. Logo, a soma valerá: S = a1 / (1 – q) = (1 /2) / 1 – (1 /2) = 1
Então, x1/2 + 1 / 4 + 1/8 + 1/16 + ... = x1 = x
5) (UEFS) Os números que expressam os ângulos de um quadrilátero, estão em progressão geométrica de razão 2. Um desses ângulos mede:
b) 32°
c) 36°
*d) 48°
e) 50°Solução:
Seja x o menor ângulo interno do quadrilátero em questão. Como os ângulos estão em Progressão Geométrica de razão 2, podemos escrever a PG de 4 termos:
( x, 2x, 4x, 8x ).
Ora, a soma dos ângulos internos de um quadrilátero vale 360º . Logo,
x + 2x + 4x + 8x = 360º
15.x = 360º
Portanto, x = 24º . Os ângulos do quadrilátero são, portanto: 24º, 48º, 96º e 192º.
O problema pede um dos ângulos. Logo, alternativa D.
6) Sabe-se que S = 9 + 99 + 999 + 9999 + ... + 999...9 onde a última parcela contém n algarismos. Nestas condições, o valor de 10n+1 - 9(S + n) é:
A)1
*B) 10
C) 100
D) -1
E) -10
*B) 10
C) 100
D) -1
E) -10
Solução:
Observe que podemos escrever a soma S como:
S = (10 – 1) + (100 – 1) + (1000 – 1) + (10000 – 1) + ... + (10n – 1)
S = (10 – 1) + (102 – 1) + (103 – 1) + (104 – 1) + ... + (10n – 1)
Como existem n parcelas, observe que o número (– 1) é somado n vezes,
resultando em n(-1) = - n.
Observe que podemos escrever a soma S como:
S = (10 – 1) + (100 – 1) + (1000 – 1) + (10000 – 1) + ... + (10n – 1)
S = (10 – 1) + (102 – 1) + (103 – 1) + (104 – 1) + ... + (10n – 1)
Como existem n parcelas, observe que o número (– 1) é somado n vezes,
resultando em n(-1) = - n.
Logo, poderemos escrever:
S = (10 + 102 + 103 + 104 + ... + 10n ) – n
S = (10 + 102 + 103 + 104 + ... + 10n ) – n
Vamos calcular a soma Sn = 10 + 102 + 103 + 104 + ... + 10n , que é uma PG de primeiro termo a1 = 10, razão q = 10 e último termo an = 10n . Teremos:
Sn = (an.q – a1) / (q –1) = (10n . 10 – 10) / (10 – 1) = (10n+1 – 10) / 9
Sn = (an.q – a1) / (q –1) = (10n . 10 – 10) / (10 – 1) = (10n+1 – 10) / 9
Substituindo em S, vem:
S = [(10n+1 – 10) / 9] – n
S = [(10n+1 – 10) / 9] – n
Deseja-se calcular o valor de 10n+1 - 9(S + n)
Temos que S + n = [(10n+1 – 10) / 9] – n + n = (10n+1 – 10) / 9
Temos que S + n = [(10n+1 – 10) / 9] – n + n = (10n+1 – 10) / 9
Substituindo o valor de S + n encontrado acima, fica:
10n+1 – 9(S + n) = 10n+1 – 9(10n+1 – 10) / 9 = 10n+1 – (10n+1 – 10) = 10
10n+1 – 9(S + n) = 10n+1 – 9(10n+1 – 10) / 9 = 10n+1 – (10n+1 – 10) = 10
7) A soma dos termos da PG (5, 50, ..., 500000) é
a) 222 222
b) 333 333
c) 444 444
d) 555 555
e) 666 666
b) 333 333
c) 444 444
d) 555 555
e) 666 666
Solução:
Para podermos aplicar a fórmula da soma dos termos de uma PG, devemos saber qual ordem do número 500000 (tercerio, quarto, décimo...). Ou seja, devemos calcular o valor de "n".
- Informações:
a1=5 q=10 an=500000
a1=5 q=10 an=500000
- Vamos aplicar a fórmula do termo geral:
an=a1·q(n-1) Substituindo seus valores
500000=5·10(n-1)
500000=5·10(n-1)
5·100000=5·10(n-1)
5·105=5·10(n-1)
105=10(n-1) Agora podemos cortar as bases
5=n-1
n=6
an=a1·q(n-1) Substituindo seus valores
500000=5·10(n-1)
500000=5·10(n-1)
5·100000=5·10(n-1)
5·105=5·10(n-1)
105=10(n-1) Agora podemos cortar as bases
5=n-1
n=6
- Agora sim, o termo 500000 é o sexto termo, podemos aplicar a fórmula da soma:
8) A razão de uma PG cujo termo geral é  é
é
a) 
b) 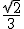
c) 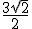
d) 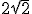
e) 
9) (PUC) De acordo com a disposição dos números abaixo,

A soma dos elementos da décima linha vale:
a) 2066
b) 5130
c) 10330
d) 20570
e) 20660
b) 5130
c) 10330
d) 20570
e) 20660
10) A seqüência 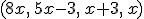 é uma progressão geométrica, de termos positivos, cuja razão é
é uma progressão geométrica, de termos positivos, cuja razão é
a) 
b) 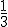
c) 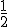
d) 
e) 
11) Dar o valor de x na igualdade x + 3x +... +729x=5465, sabendo-se que os termos do 1° membro formam uma P.G.
12) Calcule o valor de k para que a soma dos k primeiros termos da progressão geométrica (1, 3, 9, ...) seja igual a 797161.
13) As medidas do lado, do perímetro e da área de um quadrado estão em progressão geométrica, nessa ordem. A área do quadrado será:
a) 256
b) 64
c) 16
d) 243
e) 729
14) (FIA) Numa progressão geométrica, tem-se a3 = 40 e a6 = -320. A soma dos oito primeiros termos é:
a) -1700
b) -850
c) 850
d) 1700
e) 750
Gabarito:
8) A 9) C 10) C 11) x = 5 12) K = 13 13) A 14) B

Gostei do nível das questões, em geral. Sugeriria apenas, que fossem publicadas questões de vestibulares e certames mais recentes, já que as questões publicadas são antigas.
ResponderExcluirLixo esse blog
ResponderExcluirlixo....por quÊ?Ainda dá para aproveitar muita coisa boa,exemplo,essas questões de pa e pg....
ResponderExcluir