questões resolvidas de probabilidades

Exercícios resolvidos de provas anteriores de concursos e vestibulares

1) Em uma escola de idiomas com 2000 alunos, 500 alunos fazem o curso de inglês, 300 fazem o curso de espanhol e 200 cursam ambos os cursos. Selecionando-se um estudante do curso de inglês, qual a probabilidade dele também estar cursando o curso de espanhol?

a) 1/3             b) 1/4                c) 2/3                d) 2/5                 e) 3/5

Solução:

Chamemos de A o evento que representa o curso de espanhol e B o evento que representa o curso de inglês.

Podemos calcular a probabilidade de ocorrer A tendo ocorrido B através da fórmula:

Segundo o enunciado  e , então:

Note que no caso da probabilidade condicional, ao invés de calcularmos a probabilidade em função do número de elementos do espaço amostral, a calculamos em função do número de elementos do evento que já ocorreu.

A probabilidade do aluno também estar cursando o curso de espanhol é ²/_{5 letra D.}

2) Um credor está à sua procura. A probabilidade dele encontrá-lo em casa é 0,4. Se ele fizer 5 tentativas, qual a probabilidade do credor lhe encontrar uma vez em casa?

Solução:

Ou o credor vai a sua casa e o encontra, ou ele vai e não o encontra, como em cada tentativa estamos tratando de um sucesso ou de um fracasso e não há outra possibilidade, além do fato de a probabilidade ser a mesma em todas as tentativas, vamos resolver o problema utilizando o termo geral do Binômio de Newton:

n é o número de tentativas de encontrá-lo, portanto n = 5.

k é o número de tentativas nas quais ele o encontra, portanto k = 1.

p é a probabilidade de você ser encontrado, logo p = 0,4.

q é a probabilidade de você não ser encontrado, logo q = 1 - 0,4, ou seja, q = 0,6.

Substituindo tais valores na fórmula temos:

O número binomial 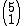 é assim resolvido:

Então temos:

Assim:

A probabilidade de o credor o encontrar uma vez em casa é igual 0,2592.

3) Em uma caixa há 4 bolas verdes, 4 azuis, 4 vermelhas e 4 brancas. Se tirarmos sem reposição 4 bolas desta caixa, uma a uma, qual a probabilidade de tirarmos nesta ordem bolas nas cores verde, azul, vermelha e branca?

Solução:

No evento E₁ a probabilidade de tirarmos uma bola verde é de 4 em 16:

Como não há reposição, a cada retirada o número de elementos do espaço amostral diminui em uma unidade.

No evento E₂ a probabilidade de tirarmos uma bola azul é de 4 em 15:

No evento E₃ a probabilidade de tirarmos uma bola vermelha é de 4 em 14:

No evento E₄ a probabilidade de tirarmos uma bola branca é de 4 em 13:

Finalmente a probabilidade de tirarmos as bolas conforme as restrições do enunciado é:

Logo:

A probabilidade é ⁸/₁₃₆₅.

4) O jogo de dominó é composto de peças retangulares formadas pela junção de dois quadrados. Em cada quadrado há a indicação de um número, representado por uma certa quantidade de bolinhas, que variam de nenhuma a seis. O número total de combinações possíveis é de 28 peças. Se pegarmos uma peça qualquer, qual a probabilidade dela possuir ao menos um 3 ou 4 na sua face?

a) 9/2            b) 11/2             c) 13/2                 d) 15/2                e) 17/2

Solução:

Chamemos de A o evento da ocorrência de um 3:

A = { (0, 3), (1, 3), (2, 3), (3, 3), (4, 3), (5, 3), (6, 3) }

Chamemos de B o evento da ocorrência de um 4:

B = { (4, 0), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6) }

Veja que o elemento (4, 3) integra os dois eventos, logo .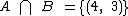

Calculando as probabilidades de A, B e da intersecção, temos:

Finalmente para o cálculo da probabilidade desejada vamos utilizar a fórmula da probabilidade da união de dois eventos:

Repare que 13 é o número total de peças que possuem 3 ou 4, desconsiderando-se a ocorrência que se repete (o (4 ,3) da intersecção dos dois eventos).

A probabilidade de ela possuir ao menos um 3 ou 4 na sua face é ¹³/₂

5) Em uma caixa há 2 fichas amarelas, 5 fichas azuis e 7 fichas verdes. Se retirarmos uma única ficha, qual a probabilidade dela ser verde ou amarela?

Solução:

Na parte teórica vimos que a probabilidade da união de dois eventos pode ser calculada através da fórmula 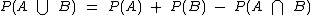 e no caso da intersecção dos eventos ser vazia, isto é, não haver elementos em comum aos dois eventos, podemos simplesmente utilizar .

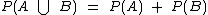Ao somarmos a quantidade de fichas obtemos a quantidade 14. Esta quantidade é o número total de elementos do espaço amostral.

Neste exercício os eventos obter ficha verde e obter ficha amarela são mutuamente exclusivos, pois a ocorrência de um impede a ocorrência do outro, não há elementos que fazem parte dos dois eventos. Não há bolas verdes que são também amarelas. Neste caso então podemos utilizar a fórmula:

Note que esta fórmula nada mais é que a soma da probabilidade de cada um dos eventos.

O evento de se obter ficha verde possui 7 elementos e o espaço amostral possui 14 elementos, que é o número total de fichas, então a probabilidade do evento obter ficha verde ocorrer é igual a ^7/₁₄:

Analogamente, a probabilidade do evento obter ficha amarela, que possui 2 elementos, é igual a ^2/₁₄:

Observe que poderíamos ter simplificado as probabilidades, quando então ^7/₁₄ passaria a ^1/₂ e ^2/₁₄ a ^1/₇, no entanto isto não foi feito, já que para somarmos as duas probabilidades precisamos que elas tenham um denominador comum:

Este exercício foi resolvido através da fórmula da probabilidade da união de dois eventos para que você tivesse um exemplo da utilização da mesma e pudesse aprender quando utilizá-la, mas se você prestar atenção ao enunciado, poderá ver que poderíamos tê-lo resolvido de uma outra forma, que em alguns casos pode tornar a resolução mais rápida. Vejamos:

Note que a probabilidade de se obter ficha azul é 5 em 14, ou seja, ^5/₁₄. Então a probabilidade de não se obter ficha azul é 9 em 14, pois:

O 1 que aparece na expressão acima se refere à probabilidade do espaço amostral.

Note que utilizamos o conceito de evento complementar, pois se não tivermos uma ficha azul, só poderemos ter uma ficha verde ou uma ficha amarela, pois não há outra opção.

A probabilidade de ela ser verde ou amarela é ⁹/₁₄.

6) Três estudantes A, B e C estão em uma competição de natação. A e B têm as mesmas chances de vencer e, cada um, tem duas vezes mais chances de vencer do que C. Pede-se calcular a probabilidades de A ou C vencer.

Solução:

Sejam p(A), p(B) e p(C), as probabilidades individuais de A, B, C, vencerem. Pelos dados do enunciado, temos:
p(A) = p(B) = 2.p(C).

Seja p(A) = k. Então, p(B) = k e p(C) = k/2.
Temos: p(A) + p(B) + p(C) = 1.

Isto é explicado pelo fato de que a probabilidade de A vencer ou B vencer ou C vencer é igual a 1. (evento certo).

Assim, substituindo, vem:

k + k + k/2 = 1 \ k = 2/5.

Portanto, p(A) = k = 2/5, p(B) = 2/5 e p(C) = 2/10 = 1/5.

A probabilidade de A ou C vencer será a soma dessas probabilidades, ou seja 2/5 + 1/5 = 3/5. 

7)  Um cartão é retirado aleatoriamente de um conjunto de 50 cartões numerados de 1 a 50. Determine a probabilidade do cartão retirado ser de um número primo.

a) 2/10              b) 3/10              c) 3/8              d) 2/8                    e) 3/20

Solução:

Os números primos de 1 a 50 são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 e 47, portanto, 15 números primos.

Temos, portanto, 15 chances de escolher um número primo num total de 50 possibilidades. 

Portanto, a probabilidade pedida será igual a p = 15/50 = 3/10.

8) Uma bola é retirada ao acaso de uma urna que contém 6 vermelhas, 4 brancas e 5 

azuis. Determinar a probabilidade dela: 

Solução:

a) ser vermelha:

P(V) = 6/15 = 2/5

b) ser branca: 

P(B) = 4/15

c) ser azul: 

P(A) = 5/15 = 1/3

d) não ser vermelha:

P=(ÑV) = 9/15 = 3/5

e) ser vermelha ou branca:

P(V ou B) = 10/15

f) de que 3 bolas sejam retiradas na ordem vermelha, branca e azul, quando cada bola 

for recolocada: P(V∩B∩A) = P(V).P(B).P(A) = (2/5).(4/15).(1/3)= 8/225 (evento indep.)

g) o mesmo, porém quando as bolas não forem recolocadas, logo:

P(V∩B∩A) = P(V).P(B|V).P(A|BV) = (6/15).(4/14).(5/13)= 4/91 (evento dep.)