QUESTÕES DE CONCURSOS, VESTIBULARES E NOTÍCIAS DE CONCURSOS EM ABERTO: Inequações 2º grau exercícios resolvidos vestibular

sábado, 10 de novembro de 2012

Inequações 2º grau exercícios resolvidos vestibular

São expressões matemáticas que apresentam os sinais de maior (>) , maior ou igual (≥ ), menor (< ), menor ou igual (≤ ) e diferente (≠) ao invés do sinal de igualdade que caracteriza as equações. Devem ser resolvidas usando a fórmula de Bháskara e comparando o resultado com o sinal da inequação, formulando assim, o resultado da inequação.

Veja alguns exemplos resolvidos para melhor compreensão:

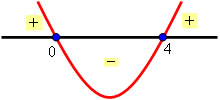
Ex1: Determine a solução da inequação x² – 4x ≥ 0.

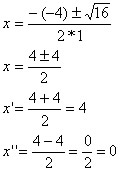
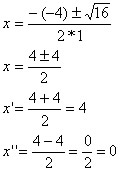
Ex2: Calcule a solução da inequação x² – 6x + 9 > 0.

S = {x Є R / x <> 3}

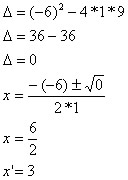
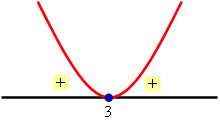
Ex3:

Achando as raízes da função, temos

E o estudo do sinal (a função é côncava para baixo, pois a < 0):

A solução é .

Exercício resolvido

Resolver a seguinte inequação: $-8 \le x^2-2x-8 \le 0$ .

Então, queremos que: $\left \{ \begin{matrix} -8 \le x^2-2x-8 \\ x^2-2x-8 \le 0 \end{matrix} \right.$

$\left \{ \begin{matrix} -8 \le x^2-2x-8 \\ x^2-2x-8 \le 0 \end{matrix} \right. \Rightarrow \left \{ \begin{matrix} 0 \le x^2-2x-8+8 \\ x^2-2x-8 \le 0 \end{matrix} \right. \Rightarrow \left \{ \begin{matrix} 0 \le x^2-2x \\ x^2-2x-8 \le 0 \end{matrix} \right. \Rightarrow \left \{ \begin{matrix} x^2-2x \ge 0 & \left(1 \right)\\ x^2-2x-8 \le 0 & \left(2 \right)\end{matrix} \right.$

Resolvendo (2): $x^2-2x-8 \le 0$ , obtemos que: $a = 1 > 0 \,\!$ ; $\Delta = 36 > 0 \,\!$ ; $x_1 = 4 \,\!$ e $x_2 = -2 \,\!$ .

Resolvendo (1): $x^2-2x \ge 0$ , obtemos que: $a = 1 > 0 \,\!$ ; $\Delta = 4 > 0 \,\!$ ; $x_1 = 2 \,\!$ e $x_2 = 0 \,\!$ .

Como temos duas soluções que devem ser satisfeitas simultâneamente, vamos calcular a intersecção $S = S_1 \cap S_2$ :

Portanto, $S = \left \{ x \in \mathbb{R} | -2 \le x \le 0 \,\, ou \,\, 2 \le x \le 4 \right \}$ .

3 comentários:

Anônimo3 de novembro de 2013 às 12:36
veleu ;D
ResponderExcluir
Respostas
Unknown4 de junho de 2016 às 01:55
Gostaria de ver esses exercícios resolvidos analiticamente
ResponderExcluir
Respostas