questões resolvidas de concursos Diagramas lógicos

Artigo com questões resolvidas de concursos sobre Diagramas lógicos extraídas de provas anteriores.

1) (ESAF) Todos os alunos de matemática são, também, alunos de inglês, mas nenhum aluno de inglês é aluno de história. Todos os alunos de português são também alunos de informática, e alguns alunos de informática são também alunos de história. Como nenhum aluno de informática é aluno de inglês, e como nenhum aluno de português é aluno de história, então:

a) pelo menos um aluno de português é aluno de inglês.
b) pelo menos um aluno de matemática é aluno de história.
c) nenhum aluno de português é aluno de matemática.
d) todos os alunos de informática são alunos de matemática.
e) todos os alunos de informática são alunos de português.

Solução:

Temos, do enunciado, as seguintes proposições:
1. Todos os alunos de matemática são, também, alunos de inglês
2. Nenhum aluno de inglês é aluno de história
3. Todos os alunos de português são também alunos de informática
4. Alguns alunos de informática são também alunos de história
5. Nenhum aluno de informática é aluno de inglês
6. Nenhum aluno de português é aluno de história

Agora iremos representar cada proposição utilizando os diagramas lógicos. Como não há uma ordem a ser seguida,podemos começar com qualquer uma das proposições até que façamos a representação de todas elas. Após desenharmos os diagramas para cada proposição, chegamos ao seguinte resultado:




Analisando as alternativas e comparando-as com os desenhos acima, vemos claramente, que o item correto é o C.

2) (Fiscal Trabalho ESAF) Maria tem três carros: um Gol, um Corsa e um Fiesta. Um dos carros é branco, o outro é preto, e o outro é azul. Sabe-se que:
1) ou o Gol é branco, ou o Fiesta é branco, 2) ou o Gol é preto, ou o Corsa é azul, 3) ou o Fiesta é azul, ou o Corsa é azul, 4) ou o Corsa é preto, ou o Fiesta é preto. Portanto, as cores do Gol, do Corsa e do Fiesta são, respectivamente,

a) branco, preto, azul
b) preto, azul, branco
c) azul, branco, preto
d) preto, branco, azul
e)) branco, azul, preto

Solução:


O enunciado informa que:
- Maria tem três carros: um Gol, um Corsa e um Fiesta.
- Um dos carros é branco, o outro é preto, e o outro é azul.

Também temos, no enunciado, as seguintes premissas:
P1: ou o Gol é branco, ou o Fiesta é branco.
P2: ou o Gol é preto, ou o Corsa é azul.
P3: ou o Fiesta é azul, ou o Corsa é azul.
P4: ou o Corsa é preto, ou o Fiesta é preto.
Para resolvermos esta questão, devemos:
1º) considerar todas as premissas verdadeiras;
2º) atribuir um valor lógico (V ou F) para uma das proposições simples; e
3º) Finalmente, substituir este valor lógico (escolhido no passo anterior) nas premissas e
verificar se está correto, ou seja, se não vai se observar alguma contradição entre os
resultados obtidos.


Vamos escolher a proposição Fiesta é branco que aparece na 1ª premissa, e atribuir o
valor lógico V. Vamos executar os seguintes passos, mostrados abaixo, para testar esta
hipótese criada por nós, ou seja, para sabermos se está certo que Fiesta é branco é V.

 Teste da hipótese: Fiesta é branco é V.
1º. F 1º. V
P1. ou o Gol é branco, ou o Fiesta é branco.
4º. F 3º. V
P2. ou o Gol é preto, ou o Corsa é azul.
1º. F 2º. V
P3. ou o Fiesta é azul, ou o Corsa é azul.
3º. F 1º. F
P4. ou o Corsa é preto, ou o Fiesta é preto.

1º passo) Da hipótese Fiesta é branco é V (em P1), e como cada carro possui cores
diferentes, teremos: Gol é branco é F (em P1), Fiesta é azul é F (em P3) e
Fiesta é preto é F (em P4).
2º passo) P3 deve ser verdadeira, daí Corsa é azul é V.
3º passo) Atribuir: Corsa é preto é F (em P4) e Corsa é azul é V (em P2).
4º passo) P2 é uma disjunção exclusiva, daí Gol é preto tem que ser F.
Houve alguma contradição entre os resultados obtidos? Claro que sim, pois obtemos
que o Gol não é preto, nem branco e nem azul! Daí, a hipótese Fiesta é branco é Falsa!
Vamos estabelecer outra hipótese (com relação ao Fiesta): Fiesta é preto é Verdade!

 Teste da hipótese: Fiesta é preto é V.
2º. V 1º. F
P1. ou o Gol é branco, ou o Fiesta é branco.
1º. F 3º. V
P2. ou o Gol é preto, ou o Corsa é azul.
1º. F 3º. V
P3. ou o Fiesta é azul, ou o Corsa é azul.
1º. F 1º. V
P4. ou o Corsa é preto, ou o Fiesta é preto.


1º passo) A hipótese é Fiesta é preto é V (em P4), e como cada carro deve ter cor
diferente, teremos: Corsa é preto é F (em P4), Fiesta é branco é F (em P1), Gol
é preto é F (em P2) e Fiesta é azul é F (em P3).
2º passo) P1 deve ser verdadeira, daí Gol é branco é V.
3º passo) P2 e P3 devem ser verdadeiras, daí Corsa é azul é V.

Houve alguma contradição entre os resultados obtidos? Agora não houve!

Resultados obtidos:
Fiesta é preto!
Gol é branco!
Corsa é azul!
Portanto, a resposta é a alternativa E.


3) (AFRE MG 2005 ESAF) Se André é culpado, então Bruno é inocente. Se André é
inocente, então Bruno é culpado. Se André é culpado, Leo é inocente. Se André é
inocente, então Leo é culpado. Se Bruno é inocente, então Leo é culpado. Logo,
André, Bruno e Leo são, respectivamente:

a) Culpado, culpado, culpado.
b) Inocente, culpado, culpado.
c)) Inocente, culpado, inocente.
d) Inocente, inocente, culpado.
e) Culpado, culpado, inocente.

Solução:

vamos utilizar o método do encadeamento das premissas.

Temos, no enunciado, as seguintes premissas:
P1: Se André é culpado, então Bruno é inocente.
P2: Se André é inocente, então Bruno é culpado.
P3: Se André é culpado, então Leo é inocente.
P4: Se André é inocente, então Leo é culpado.
P5: Se Bruno é inocente, então Leo é culpado.


Vamos atribuir letras as proposições simples;
A = André é inocente
B = Bruno é inocente
L = Leo é inocente
Traduzindo as premissas para a forma simbólica, obteremos:
P1: ~A → B
P2: A → ~B
P3: ~A → L
P4: A → ~L
P5: B → ~L

Agora, vamos efetuar o encadeamento das premissas. Da aula passada, vimos que não
há uma regra para a seqüência em que ficarão as premissas, devemos fazer por tentativa e
erro, e modificando as premissas de forma que a segunda parte da condicional de uma
premissa seja igual à primeira parte da condicional da premissa seguinte.
Para modificar as proposições condicionais devemos utilizar a regra de equivalência:
(p → q) = (~q → ~p). (Podemos memorizar essa equivalência com as palavras inverte e
troca. Vejamos: inverte-se a ordem das proposições e trocam-se os sinais. Daí, apenas
inverte e troca!)

Vamos tentar montar o quebra-cabeça:
- Vamos iniciar pelo equivalente condicional de P2: B → ~A
- Depois da P2 vamos colocar a premissa P1: ~A → B
- Depois da P1 vamos colocar a premissa P5: B → ~L
- Depois da P5 vamos colocar o equivalente condicional de P3: ~L → A
- Finalmente, depois da P4 vamos colocar a premissa P4: A → ~L

Assim, teremos o seguinte encadeamento:
B → ~A → B → ~L → A → ~L
Uma vez que estamos trabalhando apenas com estruturas condicionais, devemos
lembrar que a única situação inadmissível para uma condicional é V na primeira parte e F na

segunda. Assim, de modo que nunca ponhamos um V antes de um F, teremos os seguintes 

possíveis valores lógicos a serem analisados:

1ª 2ª 3ª 4ª 5ª 6ª
B → ~A → B → ~L → A → ~L
1ª linha: V V V V V V
2ª linha: F V V V V V
3ª linha: F F V V V V
4ª linha: F F F V V V
5ª linha: F F F F V V
6ª linha: F F F F F V
7ª linha: F F F F F F

Vamos analisar qual dessas linhas lógicas é aceitável.
- Análise da 1ª linha:
Na 2ª coluna de valores lógicos ~A é V e na 5ª coluna A também é V. Isto é
impossível! Daí devemos descartar esta 1ª linha!
- Análise da 2ª linha:
Devemos descartar essa linha pelo mesmo motivo dado na análise da 1ª linha!
- Análise da 3ª linha:
Na 1ª coluna de valores lógicos B é F e na terceira coluna B é V. Isto é impossível! Daí
devemos descartar esta 3ª linha!
- Análise da 4ª linha:
Não há contradições entre os valores lógicos, então mantemos esta linha!
- Análise da 5ª linha:
Na 4ª coluna de valores lógicos ~L é F e na sexta coluna ~L é V. Isto é impossível! Daí
devemos descartar esta 5ª linha!
- Análise da 6ª linha:
Devemos descartar essa linha pelo mesmo motivo dado na análise da 5ª linha!
- Análise da 7ª linha:
Devemos descartar essa linha pelo mesmo motivo dado na análise da 5ª linha!
Da 4ª linha que restou, obtemos os seguintes valores lógicos:
A é V , daí: André é inocente!
B é F , daí: Bruno é culpado!
~L é F (e L é V) , daí: Leo é inocente!
Portanto, a resposta é a alternativa C.


4) (Fiscal do Trabalho 2003 ESAF) Investigando uma fraude bancária, um famoso
detetive colheu evidências que o convenceram da verdade das seguintes
afirmações:
1) Se Homero é culpado, então João é culpado.
2) Se Homero é inocente, então João ou Adolfo são culpados.
3) Se Adolfo é inocente, então João é inocente.
4) Se Adolfo é culpado, então Homero é culpado.

As evidências colhidas pelo famoso detetive indicam, portanto, que:
a) Homero, João e Adolfo são inocentes.
b)) Homero, João e Adolfo são culpados.
c) Homero é culpado, mas João e Adolfo são inocentes.
d) Homero e João são inocentes, mas Adolfo é culpado.
e) Homero e Adolfo são culpados, mas João é inocente.

Solução:

Temos, no enunciado, as seguintes premissas:
P1: Se Homero é culpado, então João é culpado.
P2: Se Homero é inocente, então João ou Adolfo são culpados.
P3: Se Adolfo é inocente, então João é inocente.
P4: Se Adolfo é culpado, então Homero é culpado.
Os passos de resolução são os mesmos já nossos conhecidos.
Vamos escolher a proposição Homero é culpado que aparece na 1ª e 4ª premissas, e
atribuir o valor lógico V. Executaremos os seguintes passos abaixo, para testar esta hipótese
criada por nós, ou seja, para sabermos se está certo que Homero é culpado é V.

Teste da hipótese: Homero é culpado é V.
1º. V 2º. V
P1. Homero é culpado → João é culpado.
1º. F 3º. F
P2. Homero é inocente → (João ou Adolfo são culpados)
4º. F 3º. F
P3. Adolfo é inocente → João é inocente.
5º. V 1º. V
P4. Adolfo é culpado → Homero é culpado.

1º passo) Da hipótese Homero é culpado é V (em P1 e P4), teremos que: Homero é
inocente é F (em P2).
2º passo) P1 deve ser verdadeira, daí João é culpado tem que ser V.
3º passo) Como João é culpado é V, em P3 vamos atribuir a João é inocente o valor F e
na premissa P2 a disjunção João ou Adolfo são culpados vai ter valor V.
4º passo) P3 deve ser verdadeira, daí Adolfo é inocente tem que ser F.
5º passo) Como Adolfo é inocente é F, em P4 atribuiremos a Adolfo é culpado o valor V.
Resultados obtidos: Homero é culpado!
João é culpado!
Adolfo é culpado!
Não houve contradição entre os resultados obtidos! E todas as premissas assumiram o
valor lógico verdade!
Portanto, a resposta é a alternativa B.

5) (VUNESP/2011- Concurso TJM-SP – Analista de Sistemas (Judiciário)Todo PLATZ que não é PLUTZ é também PLETZ. Alguns PLATZ que são PLETZ também são PLITZ. A partir dessas afirmações, pode-se concluir que

a) alguns PLITZ são PLETZ e PLATZ.

b) existe PLATZ que não é PLUTZ nem é PLETZ

c) não existe PLUTZ que é apenas PLUTZ.

d) todo PLITZ é PLETZ.

e) existe PLITZ que é apenas PLITZ.

Solução:

Proposições:

• Todo Platz que não é Plutz é também Pletz. Ou seja, Platz e Pletz são duas coisas ao mesmo tempo.
• Alguns Platz também são Plitz. Ou seja, o Plitz pode ser Platz, mas isso não é uma regra geral.
• A letra E é falsa porque não existe delimitação para o conjunto Plitz e ele não fica sozinho;
• A letra B também está errada porque afima que existe Platz que não é Plutz nem é Pletz. Mas a afirmação do enunciado garante que "Todo Platz que não é Plutz é também Pletz."
• A letra C está incorreta porque essa afirmação não é dita em nenhum momento do enunciado.
• A letra D está incorreta porque não há uma regra em relação a isso também.

6) (CESPE/2011 – Concurso PC-ES – Cargos de Nível Superior) Uma pesquisa de rua feita no centro de Vitória constatou que, das pessoas entrevistadas, 60 não sabiam que a polícia civil do Espírito Santo possui delegacia com sistema online para registro ou denúncia de certos tipos de ocorrência e 85 não sabiam que uma denúncia caluniosa pode levar o denunciante à prisão por 2 a 8 anos, além do pagamento de multa. A partir dessas informações, julgue o item seguinte. Considerando-se que também foi constatado que 10 dos entrevistados não sabiam do canal de comunicação online nem das penalidades cabíveis a denúncias caluniosas, é correto concluir que 135 pessoas não tinham conhecimento de pelo menos uma dessas questões.

(     ) Certo

(     ) Errado

Solução:

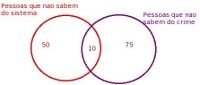
• Pessoas que não sabiam do sistema e nem das penalidades=10
• Retire essas 10 pessoas do número fornecido pelo enunciado para aquelas que não sabiam do sistema=60
• O resultado é 135, pois ao somarmos 60+85-10=135.

Gabarito das Questões	Resposta Certa
Questão 1	Letra E
Questão 2	Letra D
Questão 3	Letra A
Questão 4	Letra E
Questão 5	Letra E
Questão 6	Certa