Para resolvermos as equações logarítmicas devemos recorrer as propriedades dos logaritmos:
logbx = a, onde x = ba
Exercícios resolvidos
1) log2x + log2 (x – 2) = log228
Restrição:
x > 0
x – 2 > 0
x > 2
Restrição:
x > 0
x – 2 > 0
x > 2
log2x + log2 (x – 2) = log228
log2 x * (x – 2) = log228
x * (x – 2) = 8
x² – 2x – 8 = 0
Aplicando o Teorema de Bháskara
∆ = 36
x’ = 4
x’’ = – 2
De acordo com as restrições, devemos considerar somente x = 4, tornando a solução verdadeira.
log2 x * (x – 2) = log228
x * (x – 2) = 8
x² – 2x – 8 = 0
Aplicando o Teorema de Bháskara
∆ = 36
x’ = 4
x’’ = – 2
De acordo com as restrições, devemos considerar somente x = 4, tornando a solução verdadeira.
2) log4(x – 3) = log4(– x + 7)
restrição:
x - 3 > 0
x = > 3
- x + 7 > 0
- x > - 7 * ( - 1)
x > 7
x – 3 = – x + 7
x + x = 7 + 3
2x = 10
x = 10/2
x = 5
x + x = 7 + 3
2x = 10
x = 10/2
x = 5
3) 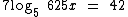
Neste caso temos a seguinte condição de existência:
Voltando à equação temos:
Aplicando a mesma propriedade que aplicamos nos casos anteriores e desenvolvendo os cálculos temos:
Como 25 satisfaz a condição de existência, então S = {25} é o conjunto solução da equação.
Se quisermos recorrer a outras propriedades dos logaritmos também podemos resolver este exercício assim:
Lembre-se que 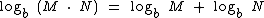 e que log5 625 = 4, pois 54 = 625.
e que log5 625 = 4, pois 54 = 625.
4) Encontre a solução da equação

Solução: Pela definição de logaritmo temos:
5x + 2 = 33
5x + 2 = 27
5x = 27 – 2
5x = 25
x = 5
Portanto S = {5}.
5) Resolva a seguinte equação:
Solução:
Solução: Pela definição de logaritmo temos:
5x + 2 = 33
5x + 2 = 27
5x = 27 – 2
5x = 25
x = 5
Portanto S = {5}.
5) Resolva a seguinte equação:
 |
Solução:
Novamente um problema que parece ser extraordinário, mas que um pouco de planejamento se torna banal:
O segredo deve estar em "remover" o exponencial em logaritmo na base 3. Pela fórmula (I) talvez alguma coisa possa ser feita. Se o primeiro membro inteiro fosse um logaritmo, o exponencial poderia "sair". Ora deve-se então transformar o primeiro membro em um logaritmo e de preferência na base 3 e para fazer isso o segundo membro deve ser transformado em um log:
Segundo a fórmula de multiplicação:
Como e e usando-se (I) nos 2 outros elementos:
e e usando-se (I) nos 2 outros elementos:
Veja que já se ilumina o fim do túnel, substituindo por y o :
:
Cujas soluções são e
e  substituindo por
substituindo por  :
:
e
6) Resolver a equação logarítmica log2x + log2 (x – 2) = log228
Restrição:
x > 0
x – 2 > 0
x > 2
log2x + log2 (x – 2) = log228
log2 x * (x – 2) = log228
x * (x – 2) = 8
x² – 2x – 8 = 0
Aplicando Bháskara
∆ = 36
x’ = 4
x’’ = – 2
De acordo com as restrições, devemos considerar somente x = 4, tornando a solução verdadeira.
O segredo deve estar em "remover" o exponencial em logaritmo na base 3. Pela fórmula (I) talvez alguma coisa possa ser feita. Se o primeiro membro inteiro fosse um logaritmo, o exponencial poderia "sair". Ora deve-se então transformar o primeiro membro em um logaritmo e de preferência na base 3 e para fazer isso o segundo membro deve ser transformado em um log:
 |
Segundo a fórmula de multiplicação:
 |
 |
Como
 e e usando-se (I) nos 2 outros elementos:
e e usando-se (I) nos 2 outros elementos: |
Veja que já se ilumina o fim do túnel, substituindo por y o
 :
: |
Cujas soluções são
 e
e  substituindo por
substituindo por  :
: |
e
 |
Restrição:
x > 0
x – 2 > 0
x > 2
log2x + log2 (x – 2) = log228
log2 x * (x – 2) = log228
x * (x – 2) = 8
x² – 2x – 8 = 0
Aplicando Bháskara
∆ = 36
x’ = 4
x’’ = – 2
De acordo com as restrições, devemos considerar somente x = 4, tornando a solução verdadeira.
7) Resolva a equação logarítmica log x + 2 (2x² + x) = 1
Restrição:
x + 2 > 0
x > – 2
x + 2 ≠ 1
x ≠ 1 – 2
x ≠ – 1
2x² + x > 0
x*(2x + 1) > 0
x > 0
2x + 1 > 0
2x > – 1
x > –1/2
Resolução:
log x + 2 (2x² + x) = 1
2x² + x = (x + 2)¹
2x² + x = x + 2
2x² + x – x – 2 = 0
2x² – 2 = 0
2x² = 2
x² = 2/2
x² = 1
√x² = √1
x’ = – 1
x’’ = 1
De acordo com as restrições entre os resultados x’ = 1 e x’’ = –1, temos que considerar somente x = 1, de forma a tornar o conjunto solução verdadeiro.
Muito Bom!!!!!!
ResponderExcluir*****
ResponderExcluirsó não entendi onde foi parar o logaritmando 28 do exemplo 1 e de onde surgiu aquele 8
ResponderExcluirTambém não entendi. Talvez seja erro de digitação?
ExcluirOs logs foram "cortados", pois eles estão em lados opostos da igualdade! (falando de maneira informal)
ExcluirPq o 7 q tá multiplicando o log na base 5 passa dividindo o 42? Que propriedade é essa?
ResponderExcluirTambém não sabia dessa
Excluir